三线合一逆定理能直接用吗

考试中不能直接使用，会扣一些分，最好是证明一下。如果是已知是中线，又是高线，那就是垂直平分线，根据定理（垂直平分线上的点到角两边的距离相等），所以两边相等。

三线合一的逆定理的应用

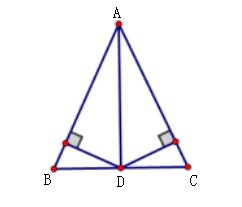
如图，①AD⊥BC于D，②AD平分∠BAC，③AD是BC中线

(1)若以①②为条件，求证AB=AC。理由如下：

∵∠ADB=∠ADC=90°，∠BAD=∠CAD，AD=AD，

∴△ABD≌△ACD(ASA)

∴AB=AC

(2)若以②③为条件，求证AB=AC。理由如下：

∵AD是BC中线，

∴S△ABD=S△ACD，

作DE⊥AB于E，DF⊥AC于F，

又∵AD平分∠BAC，

∴DE=DF，

∴AB=AC(等底等高)

(3)若①③，求证AB=AC。理由如下：

∵BD=CD，∠ADB=∠ADC=90°，AD=AD，

∴△ABD≌△ACD，

∴AB=AC